Programming in Forth is more of an “art” than programming in any other language. Like painters drawing brushstrokes, Forth programmers have complete control over where they are going and how they will get there. Charles Moore has written, “A good programmer can do a fantastic job with Forth; a bad programmer can do a disastrous job.” A good Forth programmer must be conscious of “style.”
Forth style is not easily taught; it’s a subject that deserves a book of its own. Some elements of good Forth style include:
- simplicity,
- the use of many short definitions rather than a few longer ones,
- a correspondence between words and easy-to-understand actions or data structures,
- well-chosen names, and
- well laid-out files, clearly commented.
One good way to learn style, aside from trial and error, is to study existing Forth applications, including Forth itself. In this book we’ve included the definitions of many Forth system words, and we encourage you to continue this study on your own.
This chapter introduces a classic application, the Conical Piles Calculator, which should serve as an example of good Forth style.
This example demonstrates the way to translate a mathematical equation into a Forth definition; you will see that working with fixed-point arithmetic does not necessarily mean sacrificing speed and compactness.
No Weighting
Our classic example is a math problem that many people would assume could only be solved by using floating point. It will illustrate how to handle a fairly complicated equation with fixed-point arithmetic and demonstrate that for all the advantages of using fixed-point, range and precision need not suffer. Using fixed-point has the slight disadvantage that, in order to correctly compute scale factors, we have to know our Forth’s number of bits per cell. For modern Forths the number of bits per cell can be 16, 32, 64, or even higher. In order not to complicate the following description too much, we will assume 16-bit hardware. That is probably the only environment this example will be useful for, anyway. Also, we’ll assume 1 CHARS is equivalent to one byte.
In this example we will compute the weight of a cone-shaped pile of material, knowing the height of the pile, the angle of the slope of the pile, and the density of the material.
To make the example more “concrete,” let’s weigh several huge piles of sand, gravel, and cement. The slope of each pile, called the “angle of repose,” depends on the type of material. For example, sand piles itself more steeply than gravel.

(In reality these values vary widely, depending on many factors; we have chosen approximate angles and densities for purposes of illustration.)
Here is the formula for computing the weight of a conical pile h feet tall with an angle of repose of theta degrees, where D is the density of the material in pounds per cubic foot:
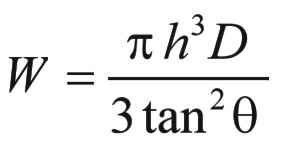
This will be the formula that we must express in Forth.
For Skeptics
The volume of a cone, V, is given by
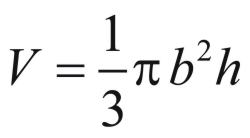
where b is the radius of the base and h is the height. We can compute the base by knowing the angle or, more specifically, the tangent of the angle. The tangent of an angle is simply the ratio of the segment marked h to the segment marked b in this drawing:
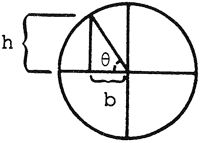
If we call this angle “theta”, then
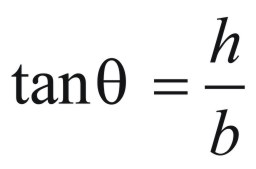
Thus we can compute the radius of the base with
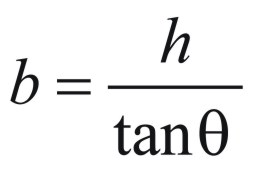
When we substitute this into the expression for V, and then multiply the result by the density D in pounds per cubic foot, we get the formula shown in the text.
Let’s design our application so that we can enter the name of a material first, such as
DRY-SAND
then enter the height of a pile and get the result for dry sand.
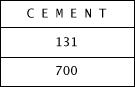
Let’s assume that for any one type of material the density and angle of repose never vary. We can store both of these values for each type of material into a table. Since we ultimately need each angle’s tangent, rather than the number of degrees, we will store the tangent. For instance, the angle of repose for a pile of cement is 35˚, for which the tangent is .700. We will store this as the integer 700.
Bear in mind that our goal is not just to get an answer; we are programming a computer or device to get the answer for us in the fastest, most efficient, and most accurate way possible. As we indicated in Chap. 5, to write equations using fixed-point arithmetic requires an extra amount of thought. But on hardware that would have to emulate floating point, the effort pays off in two ways:
- Vastly improved run-time speed, which can be very important when there are millions of steps involved in a single calculation, or when we must perform thousands of calculations every minute. Also,
- Program size, which would be critical if, for instance, we wanted to put this application in a hand-held device specifically designed as a pile-measuring calculator. Forth is often used in this type of instrument.
Let’s approach our problem by first considering scale. The height of our piles ranges from 5 to 50 feet. By working out our equation for a pile of cement 50 feet high, we find that the weight will be nearly 3,500,000 pounds.
But because our piles will not be shaped as perfect cones and because our values are averages, we cannot expect better than four or five decimal places of accuracy. If we scale our result to tons, we get about 17,500. This value will comfortably fit within the range of a single-length number, even on 16-bit hardware. For this reason, let’s write this application entirely with single-length arithmetic operators. (Although we will assume 16-bit hardware in the following, the code as shown will run unmodified on any Standard Forth system.)
Applications which require greater accuracy can be written using double-length arithmetic; to illustrate we’ve even written a second version of this application using double-length math, as you’ll see later on. But we intend to show the accuracy that Forth can achieve even with 16-bit math.
By running another test with a pile 40 feet high, we find that a difference of one-tenth of a foot in height can make a difference of 25 tons in weight. So we decide to scale our input to feet and inches rather than merely to whole feet.
We’d like the user to be able to enter
15 FOOT 2 INCH PILE
where the words FOOT and INCH will convert the feet and inches into tenths of an inch, and PILE will do the calculation. Here’s how we might define FOOT and INCH:
: FOOT 10 * ;
: INCH 100 12 */ 5 + 10 / + ;
The use of INCH is optional.
(By the way, we could as easily have designed input to be in tenths of an inch with a decimal point, like this:
15.2
In this case, NUMBER would convert the input as a double-length value. Since we are only doing single-length arithmetic, PILE could simply begin with DROP, to eliminate the high-order cell.)
In writing the definition of PILE, we must try to maintain the maximum number of places of precision without overflowing 15 bits. According to the formula, the first thing we must do is cube the argument. But let’s remember that we will have an argument which may be as high as 50 feet, which will be 500 as a scaled integer. Even to square 500 produces 250,000, which exceeds the capacity of single-length arithmetic using 16-bit cells.
We might reason that, sooner or later in this calculation, we’re going to have to divide by 2000 to yield an answer in tons. Thus the phrase
DUP DUP 2000 */
will square the argument and convert it to tons at the same time, taking advantage of */’s double-length intermediate result. Using 500 as our test argument, the above phrase will yield 125.
But our pile may be as small as 5 feet, which when squared is only 25. To divide by 2000 would produce a zero in integer arithmetic, which suggests that we are scaling down too much.
To retain the maximum accuracy, we should scale down no more than necessary. 250,000 can be safely accommodated by dividing by 10. Thus we will begin our definition of PILE with the phrase
DUP DUP 10 */
The integer result at this stage will be scaled to one place to the right of the decimal point (25000 for 2500.0).
Now we must cube the argument. Once again, straight multiplication will produce a double-length 32-bits result, so we must use */ to scale down. We find that by using 1000 as our divisor, we can stay just within single-length range. Our result at this stage will be scaled to one place to the left of the decimal point (12500 for 125000.) and still be accurate to 5 digits.
According to our formula, we must multiply our argument by pi. We know that we can do this in Forth with the phrase
355 113 */
which causes no problems with scaling.
Next we must divide our argument by the tangent squared, which we can do by dividing the argument by the tangent twice. Because our tangent is scaled to three decimal places, to divide by the tangent we multiply by 1000 and divide by the table value. Thus we will use the phrase
1000 TAN(THETA) */
Since we must perform this twice, let’s make it a definition, called /TAN (for divide-by-the-tangent) and use the word /TAN twice in our definition of PILE. Our result at this point will be scaled to one place to the left of the decimal (26711 for 267110, using our maximum test values).
All that remains is to multiply by the density of the material, of which the highest is 131 pounds per cubic foot. To avoid overflowing, let’s try scaling down by two decimal places with the phrase
DENSITY 100 */
But by testing, we find that the result at this point for a 50-foot pile of cement will be 34,991, which just exceeds the 15-bit limit. Now is a good time to take the 2000 into account. Instead of
DENSITY 100 */
we can say
DENSITY 200 */
and our answer will now be scaled to whole tons.
Program source
\ "No Weighting" from Starting Forth Chapter 12
VARIABLE DENSITY
VARIABLE THETA
VARIABLE ID
: " ( -- addr ) [CHAR] " WORD DUP C@ 1+ ALLOT ;
: MATERIAL ( addr n1 n2 -- ) \ addr=string, n1=density, n2=theta
CREATE , , ,
DOES> ( -- ) DUP @ THETA !
CELL+ DUP @ DENSITY ! CELL+ @ ID ! ;
: .SUBSTANCE ( -- ) ID @ COUNT TYPE ;
: FOOT ( n1 -- n2 ) 10 * ;
: INCH ( n1 -- n2 ) 100 12 */ 5 + 10 / + ;
: /TAN ( n1 -- n2 ) 1000 THETA @ */ ;
: PILE ( n -- ) \ n=scaled height
DUP DUP 10 */ 1000 */ 355 339 */ /TAN /TAN
DENSITY @ 200 */ ." = " . ." tons of " .SUBSTANCE ;
\ table of materials
\ string-address density tan[theta]
" cement" 131 700 MATERIAL CEMENT
" loose gravel" 93 649 MATERIAL LOOSE-GRAVEL
" packed gravel" 100 700 MATERIAL PACKED-GRAVEL
" dry sand" 90 754 MATERIAL DRY-SAND
" wet sand" 118 900 MATERIAL WET-SAND
" clay" 120 727 MATERIAL CLAY
Here’s an example of our application’s output:
CEMENT↵ ok 10 FOOT PILE↵ = 138 tons of cement ok 10 FOOT 3 INCH PILE↵ = 151 tons of cement ok DRY-SAND↵ ok 10 FOOT PILE↵ = 81 tons of dry sand ok
A note on “
The defining word MATERIAL takes three arguments for each material, one of which is the address of a string. .SUBSTANCE uses this address to type the name of the material.
To put the string in the dictionary and to give an address to MATERIAL, we have defined a word called “. As you can see from its definition, ” compiles the string (delimited by a second quotation mark) into the dictionary, with the count in the first byte, and leaves its address on the stack for MATERIAL. To compile the count and string into the dictionary, we simply have to execute WORD, since WORD’s buffer is HERE. We get the string’s address as a fillip, since WORD also leaves HERE.
All that remains is to ALLOT the appropriate number of bytes. This number is obtained by fetching the count from the first byte of the string and adding one for the count’s byte.
Chapter Summary
Review of Terms
- Stub
- in Forth, a temporary definition created solely to allow testing of a higher-level definition.
- Top-down Programming
- a programming methodology by which a large application is divided into smaller units, which may be further subdivided as necessary. The design process starts with the overview, or “top,” and proceeds down to the lowest level of detail. Coding of the low-level units begins only after the entire structure of the application has been designed.
