So far we’ve only talked about signed single-length numbers. In this chapter we’ll introduce unsigned numbers and double-length numbers, as well as a whole passel of new operators to go along with them.
This chapter is divided in two sections:
For beginners — this section explains how a computer looks at numbers and exactly what is meant by the terms signed or unsigned and by single length or double length.
For everyone — this section continues our discussion of Forth for beginners and experts alike, and explains how Forth handles signed and unsigned, single- and double-length numbers.
Section 1 — For Beginners
Signed versus Unsigned Numbers
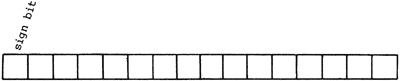
All digital computers store numbers in binary form. In Forth, the we speak of the stack in terms of the implementation’s “cell size” (common sizes are 16, 32, and 64 bits, but other cell sizes are possible). Below is a view of the least significant sixteen bits of a cell, showing the value of each bit:

If every bit were to contain a 1, the total for just these sixteen bits would be 65,535. Thus in 32 bits we can express any value between 0 and 4,294,967,295. Because this kind of number does not let us express negative values, we call it an “unsigned number.” We indicate unsigned numbers with the letter “u” in our tables and stack notations.
But what about negative numbers? In order to be able to express a positive or negative number, we need to sacrifice one bit that will essentially indicate sign. This bit is the one at the far left, the “high-order bit.” In 31 bits we can express a number as high as 2,147,483,647. When the sign bit contains 1, then we can go an equal distance back into the negative numbers. Thus within 32 bits we can represent any number from -2,147,483,648 to +2,147,483,647. This should look familiar to you as the range of a single-length number, which we denote with the letter “n.”
Before we leave you with any misconceptions, we’d better clarify the way negative numbers are represented. You might think that it’s a simple matter of setting the sign bit to indicate whether a number is positive or negative, but it doesn’t work that way.
To explain how negative numbers are represented, let’s return to decimal notation and examine a counter such as that found on many web pages.
Let’s say the counter has three digits, not five. As more people visit the page, the counter wheels turn and the number increases. Starting once again with the counter at 0, now imagine you badly regret having visited the page and could “un-visit” it by rolling the counter wheels backward. The first number you see is 999, which is, in a sense, the same as -1. The next number will be 998, which is the same as -2, and so on.
The representation of signed numbers in a computer is similar.
Starting with the 32-bit number
0000,0000,0000,0000,0000,0000,0000,0000
and going backwards one number, we get
1111,1111,1111,1111,1111,1111,1111,1111 (thirty-two ones)
which stands for 4,294,967,295 in unsigned notation as well as for -1 in signed notation. The number
1111,1111,1111,1111,1111,1111,1111,1110
which stands for 4,294,967,294 in unsigned notation, represents -2 in signed notation.
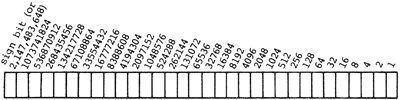
Here’s a chart that shows how a binary number on the stack can be used either as an unsigned number or as a signed number:

This bizarre-seeming method for representing negative values makes it possible for the computer to use the same procedures for subtraction as for addition.
To show how this works, let’s take a very simple problem:
2
-1
Subtracting one from two is the same as adding two plus negative one. In single-length binary notation, the two looks like this:
0000,0000,0000,0000,0000,0000,0000,0010
while negative-one looks like this:
1111,1111,1111,1111,1111,1111,1111,1111
The computer adds them up the same way we would on paper; that is when the total of any column exceeds one, it carries a one into the next column. The result looks like this:
0000,0000,0000,0000,0000,0000,0000,0010
+1111,1111,1111,1111,1111,1111,1111,1111
10000,0000,0000,0000,0000,0000,0000,0001
As you can see, the computer had to carry a one into every column all the way across, and ended up with a one in the thirty-third place. But since the stack is only thirty-two bits wide, the result is simply
0000,0000,0000,0000,0000,0000,0000,0001
which is the correct answer, one.
We needn’t explain how the computer converts a positive number to negative, but we will tell you that the process is called “two’s complementing.”
Arithmetic Shift
While we’re on the subject of how a computer performs certain mathematical operations, we’ll explain what is meant by the mysterious phrases back in Chap. 5: “arithmetic left shift” and “arithmetic right shift.”
A Forth Instant Replay:
- 2*
- ( n1 — n2 )
- Multiplies by two (arithmetic left shift).
- 2/
- ( n1 — n2 )
- Divides by two (arithmetic right shift).
To illustrate, let’s pick a number, say six, and write it in binary form:
0000,0000,0000,0000,0000,0000,0000,0110
(4+2). Now let’s shift every digit one place to the left, and put a zero in the vacant place in the one’s column.
0000,0000,0000,0000,0000,0000,0000,1100
This is the binary representation of twelve (8+4), which is exactly double the original number. This works in all cases, and it also works in reverse. If you shift every digit one place to the right and fill the vacant digit with a zero, the result will always be half of the original value.
In arithmetic shift, the sign bit does not get shifted. This means that a positive number will stay positive and a negative number will stay negative when you divide or multiply it by two.
When the high-order bit shifts with all the other bits, the term is “logical shift.” In Forth you can do a logical shift of up to 32 places with the words LSHIFT and RSHIFT.
The important thing for you to know is that most computers can shift digits much more quickly than they can go through all the folderol of normal division or multiplication. When speed is critical, it’s much better to say
2*
than
2 *
and it may even be better to say
2* 2* 2*
than
8 *
depending on your particular model of computer, but this topic is getting too technical for right now.
An Introduction to Double-Length Numbers
A double-length number is just what you probably expected it would be — a number that is represented in two cells instead of one. In a 32-bit Forth implementation, signed double-length numbers have a range of -9,223,372,036,854,775,808 to 9,223,372,036,854,775,807 (signed) or 0 to 18,446,744,073,709,551,615 (unsigned).
In Forth, a double-length number takes the place of two single-length numbers on the stack. Operators like 2DUP are useful either for double-length numbers or for pairs of single-length numbers.
One more thing we should explain: to the non-Forth-speaking computer world, the term “double word” could mean a 32-bit value, or four bytes. But in Forth, “word” means a defined command. So in order to avoid confusion, Forth programmers refer to a single number on the stack as a “cell.” A double-length number requires two cells.
Other Number Bases
As you get more involved in programming, you’ll need to employ other number bases besides decimal and binary, particularly hexadecimal (base 16) and possible octal (base 8). Since we’ll be talking about these two number bases later on in this chapter, we think you might like an introduction now.
Computer people began using hexadecimal and octal numbers for one main reason: computers think in binary and human beings have a hard time reading long binary numbers. For people, it’s much easier to convert binary to hexadecimal than binary to decimal, because sixteen is an even power of two, while ten is not. The same is true with octal. So programmers usually use hex or octal to express the binary numbers that the computer uses for things like addresses and machine codes. Hexadecimal (or simply “hex”) looks strange at first since it uses the letters A through F.
| Decimal | Binary | Hexadecimal |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Let’s take a single-length binary number:
00000000000000000111101110100001
To convert this number to hexadecimal, we first subdivide it into eight units of four bits each:
| 0000 | 0000 | 0000 | 0000 | 0111 | 1011 | 1010 | 0001 |
then convert each 4-bit unit to its hex equivalent:
|0|0|0|0|7|B|A|1|
or simply 7BA1.
Octal numbers use only the numerals 0 through 7. Because nowadays most computers use hexadecimal representation, we’ll skip an octal conversion example.
We’ll have more on conversions in the section titled “Number Conversions” later in this chapter.
The ASCII Character Set
If the computer uses binary notation to store numbers, how does it store characters and other symbols? Binary, again, but in a special code that was adopted as an industry standard many years ago. The code is called the American Standard Code for Information Interchange, usually abbreviated ASCII.
Table 7-1 shows each ASCII character in the system, its ISO 646-1983, ISO 7-bit coded character set for information interchange, International Reference Version equivalent (IRV), and its hexadecimal form.
The characters in the first column (ASCII codes 0-1F hex) are called “control characters” because they indicate that the terminal or computer is supposed to do something like ring its bell, backspace, start a new line, etc. The remaining characters are called “printing characters” because they produce visible characters including letters, the numerals zero through nine, all available symbols and even the blank space (hex 20). The only exception is DEL (hex 7F), which is a signal to the computer to ignore the last character sent.
In Chap. 1 we introduced the word EMIT. EMIT takes an ASCII code on the stack and sends it to the terminal so that the terminal will print it as a character. For example,
65 EMIT↵>A ok 66 EMIT↵B ok
etc. (We’re using the decimal, rather than the hex, equivalent because that’s what your computer is most likely expecting right now.)
Why not test EMIT on every printing character, “automatically”?
: PRINTABLES ( -- ) 127 32 DO I EMIT SPACE LOOP ;
PRINTABLES will emit every printable character in the ASCII set; that is, the characters from decimal 32 to decimal 126. (We’re using the ASCII codes as our DO loop index.)
PRINTABLES↵ ! " # $ % & ' ( ) * + , - . / ...ok
Some control (non-printing) characters that are good to know include the following:
| Name | Operation | Decimal equivalent |
| BS | Backspace | 8 |
| LF | Linefeed | 10 |
| CR | Carriage return | 13 |
Experiment with these control characters, and see what they do.
ASCII is designed so that each character can be represented by one byte. The tables in this book use the letter “c” or abbreviation “char” to indicate a byte value that is being used as a coded ASCII character.
Bit Logic
The words AND and OR (which we introduced in Chap. 4) use “bit logic”; that is, each bit is treated independently, and there are no “carries” from one bit-place to the next. For example, let’s see what happens when we AND these two binary numbers:
0000,0000,0000,0000,0000,0000,1111,1111
0000,0000,0000,0000,0110,0101,1010,0010 AND
0000,0000,0000,0000,0000,0000,1010,0010
For any result-bit to be “1,” the respective bits in both arguments must be “1.” Notice in this example that the argument on top contains all zeroes in the high-order bytes and all ones in the low-order byte. The effect on the second argument in this example is that the low-order eight bits are kept but the high-order twenty-four bits are all set to zero. Here the first argument is being used as a “mask,” to mask out the high-order bytes of the second argument.
The word OR also uses bit logic. For example,
1000,0100,0010,0001,1000,1001,0000,1001
0110,0110,0110,0110,0000,0011,1100,1000 OR
1110,0110,0110,0111,1000,1011,1100,1001
A “1” in either argument produces a “1” in the result. Again, each column is treated separately,with no carries.
By clever use of masks, we could even use a 32-bit value to hold 32 separate flags. For example,we could find out whether this bit
1000,0100,0010,0001,1000,1001,0000,1001
^
is “1” or “0” by masking out all other flags, like this:
1000,0100,0010,0001,1000,1001,0000,1001
0000,0000,0000,0000,1000,0000,0000,0000 AND
0000,0000,0000,0000,1000,0000,0000,0000
Since the bit was “1,” the result is “true.” Had it been “0,” the result would have been “0” or”false.”
We could set the flag to “0” without affecting the other flags by using this technique:
1000,0100,0010,0001,1000,1001,0000,1001
1111,1111,1111,1111,0111,1111,1111,1111 AND
1000,0100,0010,0001,0000,1001,0000,1001
We used a mask that contains all “1”s except for the bit we wanted to set to “0.” We can set the same flag back to “1” by using this technique:
1000,0100,0010,0001,0000,1001,0000,1001
0000,0000,0000,0000,1000,0000,0000,0000 OR
1000,0100,0010,0001,1000,1001,0000,1001
Section 2 — For Everybody
Signed and Unsigned Numbers
Back in Chap. 1 we introduced the word NUMBER. If the word FIND can’t find an incoming string in the dictionary, it hands it over to the word NUMBER. NUMBER then attempts to convert the string into a number expressed in binary form. If NUMBER succeeds, it pushes the binary equivalent onto the stack.
For Beginners
This means that NUMBER does not check whether the number you’ve entered as a single-length number exceeds the proper range. If you enter a giant number, NUMBER converts it but only saves the least significant thirty-two digits.
NUMBER does not do any range-checking. Because of this, NUMBER can convert either signed or unsigned numbers.
For instance, if you enter any number between 2147483648 and 4294967295, NUMBER will convert it as an unsigned number. Any value between -2147483648 and -1 will be stored as a two’s-complement integer.

This is an important point: the stack can be used to hold either signed or unsigned numbers. Whether a binary value is interpreted as signed or unsigned depends on the operators that you apply to it. You decide which form is better for a given situation, then stick to your choice.
We’ve introduced the word ., which prints a value on the stack as a signed number:
4294967295 .↵-1 ok
The word U. prints the binary representation as an unsigned number:
4294967295 U.↵4294967295 ok
- U.
- ( u — )
- Prints the unsigned single-length number, followed by a space.

In this book the letter “n” signifies signed single-length numbers, while the letter “u” signifies unsigned single-length numbers. (We’ve already introduced U.R, which prints an unsigned single-length number right-justified within a given column width.)
Here are some additional words that use unsigned numbers:
- UM*
- ( u1 u2 — ud )
- Multiplies two single-length numbers. Returns a double-length result. All values are unsigned.
- UM/MOD
- ( ud u1 — u2 u3 )
- Divides a double-length by a single-length number. Returns a single-length remainder u2 and quotient u3. All values are unsigned.
- U<
- ( u1 u2 — f )
- Leaves true if u1 < u2, where both are treated as single-length unsigned integers.
Number Bases
When you first start Forth, all number conversions use base ten (decimal), for both input and output.
You can easily change the base by executing one of the following commands:
- HEX
- ( — )
- Sets the base to sixteen.
- OCTAL
- ( — )
- Sets the base to eight (available on some systems).
- DECIMAL
- ( — )
- Sets the base to ten.
When you change the number base, its stays changed until you change it again. So be sure to declare DECIMAL as soon as you’re done with another number base.
These commands make it easy to do number conversions in “calculator style.”
For example, to convert decimal 100 into hexadecimal, enter
DECIMAL 100 HEX .↵64 ok
To convert hex F into decimal (remember you are already in hex), enter
0F DECIMAL .↵15 ok
Make it a habit, starting right now, to precede each hexadecimal value with a zero, as in
0A 0B 0F
This practice avoids mix-ups with possibly predefined words as DEADBEEF, BAD, DEC etc.
Handy Hint A definition of BINARY — or Any-ARY
Beginners who want to see what numbers look like in binary notation may enter this definition:
: BINARY ( -- ) 2 BASE ! ;
The new word BINARY will operate just like OCTAL or HEX but will change the number base to two. On systems that don’t have the word OCTAL, experimenters may define
: OCTAL ( -- ) 8 BASE ! ;
Double-Length Numbers
Most ANS Forth systems support double-length numbers to some degree. The standard way to enter a double-length number onto the stack (whether from the keyboard or from a file) is to punctuate it with a period at the end. When the text interpreter processes a number that is immediately followed by a decimal point and is not found as a definition name, it is converted to a double-cell number.
For example, when you type
200000.↵
NUMBER recognizes the period at the as a signal that this value should be converted to double-length. NUMBER then pushes the value onto the stack as two consecutive “cells” (cell is the Forth term for a single-length item on the stack), the high order cell on top.
Some Forth implementations (including SwiftForth) will convert any number that contains the following characters as a double number:
+ , - . / :
The Forth word D. prints a double-length number without any punctuation:
- D.
- ( d — )
- Prints the signed double-length number d, followed by one space.

In this book, the letter “d” stands for a double-length signed integer.
For example, having entered a double-length number, if you were now to execute D.,the computer would respond:
D.↵200000 ok
In the next section we’ll show you how to define your own equivalents to D. which will print whatever punctuation you want along with the number.
Number Formatting — Double-Length Unsigned
$200.00 12/31/80 999-6784 6:32:59 98.6
The above numbers represent the kinds of output you can create by defining your own “number-formatting words” in Forth. This section will show you how.
The simplest number-formatting definition we could write would be
: UD. ( ud -- ) <# #S #> TYPE ;
UD. will print an unsigned double-length number. The words <# and #> (respectively pronounced bracket-number and number-bracket) signify the beginning and the end of the number-conversion process. In this definition, the entire conversion is being performed by the single word #S (pronounced numbers). #S converts the value on the stack into ASCII characters. It will only produce as many digits as are necessary to represent the number; it will not produce leading zeroes. But it always produces at least one digit, which will be zero if the value was zero. For example:
12,345 UD.↵12345ok 12. UD.↵12ok 0. UD.↵0ok
The word TYPE prints the characters that represent the number at your terminal. Notice that there is no space between the number and the “ok.” To get a space,you would simply add the word SPACE, like this:
: UD. ( ud -- ) <# #S #> TYPE SPACE ;
Now let’s say we have a phone number on the stack, expressed as a double-length unsigned integer. For example, we may have typed in:
999-6784
(remember that the hyphen tells NUMBER to treat this as a double-length value). We want to define a word that will format this value back as a phone number. Let’s call it .PH# (for “print the phone number”) and define it thus:
: .PH# ( ud -- ) <# # # # # [CHAR] - HOLD #S #> TYPE SPACE ;

Our definition of .PH# has everything that UD. has, and more. The Forth word # (pronounced number) produces a single digit only. A number-formatting definition is reversed from the order in which the number will be printed, so the phrase
# # # #
produces the right-most four digits of the phone number.
Now it’s time to insert the hyphen. Using [CHAR] we can get the code value of this ASCII character on the stack. The Forth word HOLD takes this ASCII code and inserts it into the formatted number character string.
We now have three digits left. We might use the phrase
# # #
but it is easier to simply use the word #S, which will automatically convert the rest of the number for us.
Now let’s format an unsigned double-length number as a date, in the following form:
6/15/03
Here is the definition:
: .DATE ( ud -- ) <# # # [CHAR] / HOLD # # [CHAR] / HOLD #S #> TYPE SPACE ;

Let’s follow the above definition, remembering that it is written in reverse order from the output. The phrase
# # [CHAR] / HOLD
produces the right-most two digits (representing the year) and the right-most slash. The next occurrence of the same phrase produces the middle two digits (representing the day) and the left-most slash. Finally #S produces the left-most two digits(representing the month).
We could have just as easily defined
# # [CHAR] / HOLD
as its own word and used this word twice in the definition of .DATE.
Since you have control over the conversion process, you can actually convert different digits in different number bases, a feature which is useful in formatting such numbers as hours and minutes. For example, let’s say that you have the time in seconds on the stack, and you want a word which will print hh:mm:ss. You might define it this way:
: SEXTAL ( -- ) 6 BASE ! ; : :00 ( ud1 -- ud2 ) # SEXTAL # DECIMAL [CHAR] : HOLD ; : SEC ( ud -- ) <# :00 :00 #S #> TYPE SPACE ;
We will use the word :00 to format the seconds and minutes. Both seconds and minutes are modulo-60, so the right digit can go as high as nine, but the left digit can only go up to five. Thus in the definition of :00 we convert the first digit (the one on the right) as a decimal number, then go into “sextal” (base 6) and convert the left digit. Finally, we return to decimal and insert the colon character. After :00 converts the seconds and the minutes,#S converts the remaining hours.
For example, if we had 4500 seconds on the stack, we would get
4500. SEC↵1:15:00 ok
This glossary summarizes the Forth words that are used in number formatting:
- <#
- ( — )
- Begins the number conversion process.
- #
- ( ud1 — ud2 )
- Converts one digit and prepends it to the output character string. Always produces a digit — if you’re out of significant digits, you’ll still get a zero for every #.
- #S
- ( ud1 — ud2 )
- Converts the number until the result is zero. Always produces at least one digit (0 if the value is zero).
- HOLD
- ( char — )
- Inserts, at the current position in the character string being formatted, a character whose ASCII value is on the stack. HOLD (or a word that uses HOLD) must be used between <# and #>.
- SIGN
- ( n — )
- Prepends a minus sign to the output string if the top of stack is negative.
- #>
- ( ud — addr len )
- Completes number conversion by leaving the address and length of the string on the stack (these are the appropriate arguments for TYPE).
These are the stack effects for number formatting:
- <# … #>
- ( ud — addr len )
- Converts double-length unsigned value ud to output string addr len.
- <# … ROT SIGN #>
- ( n |d| — addr u )
- Converts double-length signed value (where n is the high-order cell of d and |d| is the absolute value of d).
Key to stack comment notation:
| n, n1, … | Single-length signed |
| d, d1, … | Double-length signed |
| u, u1 … | Single-length unsigned |
| ud, ud1, … | Double-length unsigned |
| addr | Address |
| len | Length (of string or buffer) |
| char | ASCII character value |
Number Formatting — Signed and Single-Length
So far we have formatted only unsigned double-length numbers. The <#…#> form expects only unsigned double-length numbers, but we can use it for other types of numbers by making certain arrangements on the stack.

For instance, let’s look at a simplified version of the system definition of D. (which prints a signed double-length number):
: D. ( d -- ) TUCK DABS <# #S ROT SIGN #> TYPE SPACE ;
The phrase ROT SIGN inserts a minus string in the character string if the third number on the stack is negative. We have prepared for this test by putting a copy of the high-order cell (the one with the sign bit) at the bottom of the stack, by using the word TUCK.
Because <# expects only unsigned double-length numbers,we must take the absolute value of our double-length signed number, with the word DABS. We now have the proper arrangement of arguments on the stack for the <#…#> phrase. In some cases, such as accounting, we may want a negative number to be written
12345-
in which case we would place the phrase ROT SIGN at the left side of our <#…#> phrase, like this:
<# ROT SIGN #S #>
Let’s define a word which will print a signed double-length number with a decimal point and two decimal places to the right of the decimal. Since this is the form most often used for writing dollars and cents, let’s call it
.$
and define it like this:
: .$ ( d -- ) TUCK DABS <# # # [CHAR] . HOLD #S ROT SIGN [CHAR] $ HOLD #> TYPE SPACE ;
Let’s try it:
2000.00 .$↵$2000.00 ok
or even
2,000.00 .$↵$2000.00 ok
We recommend that you save .$, since we’ll be using it in some future examples.
You can also write special formats for single-length numbers. For example, if you want to use an unsigned single-length number, simply put a zero on the stack before the word <#. This effectively changes the single-length number into a double-length number which is so small that it has nothing (zero) in the high-order cell. To format a signed single-length number, again you must supply a zero as a high-order cell. But you must also leave a copy of the signed number in the third stack position for ROT SIGN, and you must leave the absolute value of the number in the second stack position. The phrase to do all this is
DUP ABS 0
Here are the “set-up” phrases that are needed to print various kinds of numbers:
| Number to be printed | Precede <# by |
| Double-length, unsigned | (nothing needed) |
| Double-length, signed | SWAP OVER DABS (to save the sign for SIGN) |
| Single-length, unsigned | 0 (for high-order dummy) |
| Single-length, signed | DUP ABS 0 (to save the sign) |
Double-Length Operators
Here is a list of double-length math operators:
- D.R
- ( d u — )
- Prints the signed double-length number d, right-justified within the field width u.
- D+
- ( d1 d2 — d3 )
- Adds two double-length numbers d1 and d2, returning the sum d3
- D-
- ( d1 d2 — d3 )
- Subtracts double-length number d2 from d1, returning the difference d3.
- DNEGATE
- ( d1 — d2 )
- Changes the sign of a double-length number.
- DMAX
- ( d1 d2 — d3 )
- Returns the maximum of two double-length numbers.
- DMIN
- ( d1 d2 — d3 )
- Returns the minimum of two double-length numbers.
- D=
- ( d1 d2 — flag )
- Returns true if d1 and d2 are equal.
- D0=
- Returns true if d is zero.
- D<
- ( d1 d2 — flag )
- Returns true if d1 is less than d2. Both numbers are signed.
- DU<
- ( ud1 ud2 — flag )
- Returns true if ud1 is less than ud2. Both numbers are unsigned.
The initial “D” signifies that these operators may only be used for double-length operations, whereas the initial “2,” as in 2SWAP and 2DUP, signifies that these operators may be used either for double-length numbers or for pairs of single-length numbers.
Here’s an example using D+:
200,000 300,000 D+ D.↵500000 ok
Mixed-Length Operators
Here’s a list of very useful Forth words that operate on a combination of single- and double-length numbers:
- M+
- ( d1 n — d2 )
- Adds double-length number d1 to a single-length number n. Returns double-length result d2.
- SM/REM
- ( d n1 — n2 n3 )
- Divide d1 by n1, giving the symmetric quotient n3 and the remainder n2. Input and output stack arguments are signed. An ambiguous condition exists if n1 is zero or if the quotient lies outside the range of a single-cell signed integer.
- FM/MOD
- ( d n1 — n2 n3 )
- Divide d1 by n1, giving the floored quotient n3 and the remainder n2. Input and output stack arguments are signed. An ambiguous condition exists if n1 is zero or if the quotient lies outside the range of a single-cell signed integer.
- M*
- ( n1 n2 — d )
- Multiplies two single-length numbers. Returns a double-length result. All values are signed.
- M*/
- ( d1 n1 +n2 — d2 )
- Multiplies d1 by n1 producing the triple-cell intermediate result t. Divides t by +n2 giving the double-cell quotient d2. An ambiguous condition exists if +n2 is zero or negative, or the quotient lies outside of the range of a double-precision signed integer.
Here’s an example using M+:
200,000 7 M+ D.↵200007 ok
Or, using M*/, we can redefine our earlier version of % so that it will accept a double-length argument:
: % ( d1 -- d2 ) 100 M*/ ;
as in
200.50 15 % D.↵3007 ok
If you have loaded the definition of .$ we gave in the last Handy Hint, you can enter
200.50 15 % .$↵$30.07 ok
We can redefine our earlier definition of R% to get a rounded double-length result, like this:
: R% ( d1 -- d2 ) 10 M*/ 5 M+ 1 10 M*/ ;
then
200.50 15 R% .$↵$30.08 ok
Notice that M*/ is the only ready-made Forth word which performs multiplication on a double-length argument. To multiply 200,000 by 3, for instance, we must supply a “1” as a dummy denominator:
200,000 3 1 M*/ D.↵600000 ok
since
3
1
is the same as 3.
M*/ is also the only ready-made Forth word that performs division with a double-length result. So to divide 200,000 by 4, for instance, we must supply a “1” asa dummy numerator:
200,000 1 4 M*/ D.↵50000 ok
Numbers in Definitions
When a definition contains a number, such as
: SCORE-MORE ( n1 -- n2 ) 20 + ;
the number is compiled into the dictionary in binary form, just as it looks on the stack.
The number’s binary value depends on the number base at the time you compile the definition. For example, if you were to enter
HEX : SCORE-MORE ( n1 -- n2 ) 14 + ; DECIMAL
the dictionary definition would contain the hex value 14, which is the same as the decimal value 20 (16+4). Henceforth, SCORE-MORE will always add the equivalent of the decimal 20 to the value on the stack, regardless of the current number base.
If, on the other hand, you were to put the word HEX inside the definition, then you would change the number base when you execute the definition.
For example, if you were to define:
DECIMAL : EXAMPLE ( -- ) HEX 20 . DECIMAL ;
the number would be compiled as the binary equivalent of decimal 20, since DECIMAL was current at compilation time.
At execution time, here’s what happens:
EXAMPLE↵14 ok
The number is output in hexadecimal.
For the record, a number that appears inside a definition is called a “literal.” (Unlike the words in the rest of the definition which allude to other definitions, a number must be taken literally.)
Chapter Summary
Forth Words
Here is a list of the Forth words we’ve covered in this chapter:
- U.
- ( u — )
- Prints the unsigned single-length number, followed by a space.
- UM*
- ( u1 u2 — ud )
- Multiplies two single-length numbers. Returns a double-length result. All values are unsigned.
- UM/MOD
- ( ud u1 — u2 u3 )
- Divides a double-length by a single-length number. Returns a single-length quotient u2 and remainder u3. All values are unsigned.
- U<
- ( u1 u2 — f )
- Leaves true if u1 < u2, where both are treated as single-length unsigned integers.
- HEX
- ( — )
- Sets the base to sixteen.
- OCTAL
- ( — )
- Sets the base to eight (available on some systems).
- DECIMAL
- ( — )
- Sets the base to ten.
- <#
- ( — )
- Begins the number conversion process.
- #
- ( ud1 — ud2 )
- Converts one digit and prepends it to the output character string. Always produces a digit — if you’re out of significant digits, you’ll still get a zero for every #.
- #S
- ( ud1 — ud2 )
- Converts the number until the result is zero. Always produces at least one digit (0 if the value is zero).
- HOLD
- ( char — )
- Inserts, at the current position in the character string being formatted, a character whose ASCII value is on the stack. HOLD (or a word that uses HOLD) must be used between <# and #>.
- SIGN
- ( n — )
- Prepends a minus sign to the output string if the top of stack is negative.
- #>
- ( ud — addr len )
- Completes number conversion by leaving the address and length of the string on the stack (these are the appropriate arguments for TYPE).
- D.
- ( d — )
- Prints the signed double-length number d, followed by one space.
- D.R
- ( d u — )
- Prints the signed double-length number d, right-justified within the field width u.
- D+
- ( d1 d2 — d3 )
- Adds two double-length numbers d1 and d2, returning the sum d3
- D-
- ( d1 d2 — d3 )
- Subtracts double-length number d2 from d1, returning the difference d3.
- DNEGATE
- ( d1 — d2 )
- Changes the sign of a double-length number.
- DMAX
- ( d1 d2 — d3 )
- Returns the maximum of two double-length numbers.
- DMIN
- ( d1 d2 — d3 )
- Returns the minimum of two double-length numbers.
- D=
- ( d1 d2 — flag )
- Returns true if d1 and d2 are equal.
- D0=
- Returns true if d is zero.
- D<
- ( d1 d2 — flag )
- Returns true if d1 is less than d2. Both numbers are signed.
- DU<
- ( ud1 ud2 — flag )
- Returns true if ud1 is less than ud2. Both numbers are unsigned.
- M+
- ( d1 n — d2 )
- Adds double-length number d1 to a single-length number n. Returns double-length result d2.
- SM/REM
- ( d n1 — n2 n3 )
- Divide d1 by n1, giving the symmetric quotient n3 and the remainder n2. Input and output stack arguments are signed. An ambiguous condition exists if n1 is zero or if the quotient lies outside the range of a single-cell signed integer.
- FM/MOD
- ( d n1 — n2 n3 )
- Divide d1 by n1, giving the floored quotient n3 and the remainder n2. Input and output stack arguments are signed. An ambiguous condition exists if n1 is zero or if the quotient lies outside the range of a single-cell signed integer.
- M*
- ( n1 n2 — d )
- Multiplies two single-length numbers. Returns a double-length result. All values are signed.
- M*/
- d1 +n1 n2 — d2 )
- Multiplies double-length number d1 by single-length positive number n1 and divides the triple-length result by single-length number n2. Returns double-length result d2. All values are signed.
Review of Terms
- Arithmetic left and right shift
- the process of shifting all bits in a number, except the sign bit, to the left or right, in effect doubling or halving the (assumed signed) number, respectively.
- Logical left and right shift
- the process of shifting all bits in a number, including the sign bit, to the left or right, in effect doubling or halving the (assumed unsigned) number, respectively.
- ASCII
- a standardized system of representing input/output characters as byte values. Acronym for American Standard Code for Information Interchange. (Pronounced ask-key)
- Binary
- number base 2.
- Byte
- the standard term for an 8-bit value.
- Cell
- the Forth term for a single-cell value.
- Decimal
- number base 10.
- Hexadecimal
- number base 16.
- Literal
- in general, a number of symbol which represents only itself; in Forth, a number that appears inside a definition.
- Mask
- a value which can be ” superimposed” over another, hiding certain bits and revealing only those bits that we are interested in.
- Number formatting
- the process of printing a number, usually in a special form such as 3/13/03 or $47.93.
- Octal
- number base 8.
- Sign bit high-order bit
- the bit which, for a signed number, indicates whether it is positive or negative and, for an unsigned number, represents the bit of the highest magnitude.
- Two’s complement
- for any number, the number of equal absolute value but opposite sign. To calculate 10 – 4, the computer first produces the two’s complement of 4, (i.e., -4), then computes 10 + (-4).
- Unsigned number
- a number which is assumed to be positive.
- Unsigned single-length number
- an integer which falls within the range of 0 to 2147483647.
- Word
- In Forth, a defined dictionary entry, elsewhere, a term for a 16-bit value.
- Integer division
- produces a quotient q and a remainder r by dividing operand a by operand b. Division operations return q, r, or both. The identity b*q + r = a holds for all a and b.
- Floored division
- is integer division in which the remainder carries the sign of the divisor or is zero, and the quotient is rounded to its arithmetic floor.
- Symmetric division
- is integer division in which the remainder carries the sign of the dividend or is zero and the quotient is the mathematical quotient “rounded towards zero” or “truncated”.

Problems — Chapter 7
- Veronica Wainwright couldn’t remember the upper limit for a signed single-length number, and she had no book to refer to, only a Forth terminal. So she wrote a definition called N-MAX, using a BEGIN… UNTIL loop. When she executed it, she got
↵2147483647 okWhat was her definition?
- Since you now know that AND and OR employ bit logic, explain why the following example must use OR instead of +:
: MATCH humorous sensitive AND art-loving music-loving OR AN smoking 0= AND IF ." I have someone you should meet " THEN ;
- Write a definition that “rings” your terminal’s bell three times. Make sure that there is enough of a delay between the bells so that they are distinguishable. Each time the bell rings, the word “BEEP” should appear on the terminal screen.
- Rewrite the temperature conversion definitions you created for the problems in Chap. 5. This time assume that the input and resulting temperatures are to be double-length signed integers, which are scaled (i.e., multiplied) by ten. For example, if 10.5 degrees is entered, it is a 32-bit integer with a value of 105.
- Write a formatted output word named .DEG which will display a double-length signed integer scaled by ten as a string of digits, a decimal point, and one fractional digit. For example:
12.3 .DEG↵12.3 ok - Solve the following conversions:
0.0° F in Celsius
212.0° F in Celsius
20.0° F in Celsius
16.0° C in Fahrenheit
-40.0° C in Fahrenheit
100.0° K in Celsius
100.0° K in Fahrenheit
233.0° K in Celsius
233.0° K in Fahrenheit - Write a routine that evaluates the quadratic equation 7x2 + 20x + 5 given x, and returns a double-length result.
- Write a word .BASES that prints the numbers 0 through 16 (decimal) in decimal, hexadecimal, and binary form in three columns. E.g.,
DECIMAL 0 HEX 0 BINARY 0DECIMAL 1 HEX 1 BINARY 1DECIMAL 2 HEX 2 BINARY 10...DECIMAL 16 HEX 10 BINARY 10000
- If you enter
..↵(two periods not separated by a space) and the system responds “ok,” what does this tell you?
- Write a definition for a phone-number formatting word that will also print the area code with a slash if and only if the number includes an area code. E.g.,
555-1234 .PH# 555-1234↵ok 310/999-6784 .PH#↵310/999-6784 ok
Answers
: N-MAX ( -- n ) 0 BEGIN 1+ DUP 0< UNTIL 1- ; \ This can take a very long time on a 32-bit system.
- Using + gives an arithmetic addition of flags whereas OR performs a logical bitwise or.
: MS ( u -- ) DROP ; \ if your system doesn't have MS : BEEP ." BEEP " 7 EMIT ; \ not ANS but works on many systems : DELAY 500 MS ; : RING BEEP DELAY BEEP DELAY BEEP ;
: F>C ( d1 -- d2 ) -320 M+ 10 18 M*/ ; : C>F ( d1 -- d2 ) 18 10 M*/ 320 M+ ; : C>K ( d1 -- d2 ) 2732 M+ ; : K>C ( d1 -- d2 ) -2732 M+ ; : F>K ( d1 -- d2 ) F>C C>K ; : K>F ( d1 -- d2 ) K>C C>F ;
: .DEG ( d -- ) TUCK DABS <# # [CHAR] . HOLD #S ROT SIGN #> TYPE SPACE ;
0.0 F>C .DEG↵-17.7 ok 212.0 F>C .DEG↵100.0 ok 20.0 F>C .DEG↵-6.6 ok 16.0 C>F .DEG↵60.8 ok -40.0 C>F .DEG↵-40.0 ok 100.0 K>C .DEG↵-173.2 ok 100.0 K>F .DEG↵-279.7 ok 233.0 K>C .DEG↵-40.2 ok 233.0 K>F .DEG↵-40.3 ok
: POLY ( x -- d ) DUP 7 * 20 + M* 5 M+ ;
: BINARY 2 BASE ! ; : .BASES ( -- ) 17 0 DO CR ." decimal" DECIMAL I 4 U.R 8 SPACES ." hex " HEX I 3 U.R 8 SPACES ." binary" BINARY I 8 U.R 8 SPACES LOOP DECIMAL ;- It tells you this is a Forth system that interprets any number of decimal points as double specifiers.
: .PH# ( d -- ) <# # # # # [CHAR] - HOLD # # # OVER IF [CHAR] / HOLD #S THEN #> TYPE SPACE ;
